Centre for Discrete and Applicable Mathematics
	CDAM Research Report, LSE-CDAM-2005-08 May 2005

Dividend Policy Irrelevance and Eigenvalue Location

Adam Ostaszewski

This note gives a qualified affirmative answer to a natural question, asked by Ohlson and motivated by some earlier work, concerning the irrelevance of dividend policy to the calculation of equity in the context of an Ohlson style general linear accounting dynamic. Does Dividend Irrelevance occur when discounting at a rate of interest R if and only if R is set equal uniquely to the dominant eigenvalue of the principal submatrix? The latter submatrix relates the accounting variables to each other in the absence of any dividend payout. The question reduces to the assertion that the maximum eigenvalue  κ_max of the following `bordered diagonal matrix'

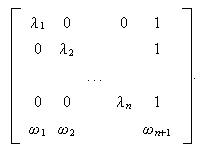
 lies between the first largest and second largest among |λ₁|,...,|λ_n|. 
An affirmative answer necessarily restricts the dividend policy vector (ω₁,..., ω_n+1). The results show that an algebraic condition equivalent to dividend irrelevance derived previously is not vacuous.

Key words: Dividend irrelevance, dominant eigenvalue, bordered diagonal matrix.

A PDF file (194 kB) with the full contents of this report can be downloaded by clicking here.

Alternatively, if you would like to get a free hard copy of this report, please send the number of this report, LSE-CDAM-2005-08, together with your name and postal address to:

		CDAM Research Reports Series Centre for Discrete and Applicable Mathematics London School of Economics Houghton Street London WC2A 2AE, U.K.
		Phone: +44(0)-20-7955 7732. Fax: +44(0)-20-7955 6877. Email: info@maths.lse.ac.uk

		Introduction to the CDAM Research Report Series.
		CDAM Homepage.

Last modified: 9th May 2005