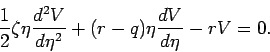Centre for Discrete and Applicable Mathematics

CDAM Research Report, LSE-CDAM-2004-13

July 2004

`Equity smirks' and embedded options: the shape of a firm's value function

Adam Ostaszewski

Abstract

This paper examines the methodology and assumptions of Ashton, D., Cooke, T.,Tippett, M., Wang, P. (2004) employing recursion value &eta as an explanatory single-variable in a model of the firm, first introduced by Ashton, D.,Cooke,T.,Tippett in (2003). A qualitative analysis of all of their numerical findings is given together with an indication of how more useful is the tool of special function theory, here requiring confluent hypergeometric functions associated with the Merton-style valuation equation

$\begin{displaymath} \frac{1}{2}\zeta \eta \frac{d^{2}V}{d\eta ^{2}}+(r-q)\eta \frac{dV}{d\eta } -rV=0. \end{displaymath}$

A justification and a wider interpretation of their model and findings is offered: these come from inclusion of strictly convex dissipating frictions arising either as insurance costs, replacement costs of funds paid out, or of debt service, and from the inclusion of alternative adaptation options embedded in the equity value of a firm; these predict not only a J-shaped equity curve, but also, under the richer modelling assumption, a snake-like curve that may result from financial frictions like insurance. These `smirks' in the equity curve may be empirically tested. It is shown that the inclusion of frictions in dividend selection (e.g. the signalling costs of Bhattacharya) leads to an optimal dividend payout of &alpha &eta that is a constant coupon for an interval of &eta values preceded by an interval in which &alpha=r; this is at variance with the ACTW model where the exogeneous assumption of a constant &alpha is made.
This is the full, detailed, version of a discussion paper presented at State of the Art International Advances in Accounting Based Valuation at the Cass Business School, a conference held in association with the journal, Accounting & Business Research, London, December 12th and 13th 2003. I am indebted to Ken Peasnell for suggesting the word `smirk'. I am grateful to Jim Ohlson, Mark Tippett, Miles Gietzmann, to colleagues at LSE, and to colleagues at University College London Mathematics Department, particularly Susan Brown and S.N. Timoshin for very helpful discussions.

A PDF file (316 kB) with the full contents of this report can be downloaded by clicking here.

Alternatively, if you would like to get a free hard copy of this report, please send the number of this report, LSE-CDAM-2004-13, together with your name and postal address to:

CDAM Research Reports Series
Centre for Discrete and Applicable Mathematics
London School of Economics
Houghton Street
London WC2A 2AE, U.K.

Phone: +44(0)-20-7955 7732.
Fax: +44(0)-20-7955 6877.
Email: info@cdam.lse.ac.uk

		Introduction to the CDAM Research Report Series.
		CDAM Homepage.

Last changed: Wed 9 Feb 2005
For comments go to: http://www.maths.lse.ac.uk/webmaster.html

		CDAM Research Reports Series Centre for Discrete and Applicable Mathematics London School of Economics Houghton Street London WC2A 2AE, U.K.
		Phone: +44(0)-20-7955 7732. Fax: +44(0)-20-7955 6877. Email: info@cdam.lse.ac.uk